How to Draw a Line Graph in Latex
Hands-on Tutorials
Using pgfplots to make economic graphs in LaTeX
An approachable guide to making sleek, professional graphs in the industry standard typesetting language
![]()
1. Introduction
Economics makes an abundant use of graphs to illustrate important concepts and phenomena. Yet the first thing one may notice when typing up a paper in the field is the difficulty of making these graphs using word processors. That is where LaTeX comes in. This guide will explain how we can use the pgfplots package to make elegant economic graphs in LaTeX.
1.1. New to LaTeX?
Some readers may be unfamiliar with La T eX. It is a powerful typesetting language capable of typesetting text, mathematical formulas, tables, and many other elements that word processors such as Word and Google Docs are incapable of. Its capabilities are extended by packages. This guide will focus on making graphs with a package designed for plotting graphs — pgfplots — which itself relies on a package designed for making graphics — TikZ.
Along with LaTeX's formidable ability and customizability comes with it a reputable learning curve. Do not despair. This guide was written under the assumption that readers are familiar with the very basics of LaTeX — but no more than that. (In Section 8: Resources, there are resources you can use to set up and learn the basics of LaTeX.) If you can create a text document, load in packages, and write an equation in LaTeX's display math mode, you need not know anything else. Although if you are already familiar with pgfplots and TikZ, you may still find some of the techniques used here useful for the very specific features of economic graphs.
1.2. GitHub project repository
All of the finished graphs shown here are available on the GitHub repository for this guide. You can access the repository at https://github.com/jackypacky/pgf-econ-graphs. There, the TeX source codes and PDFs of all the graphs can be found.
1.3. Packages
We will be using pgfplots to draw economic graphs, so the pgfplots package should be called. This will call TikZ and xcolor as well. Since we want to be able to shade in areas under curves, the fillbetween pgfplots library should be called. Since we want to be able to specify positions around coordinates and use a variety arrowheads in TikZ, the positioning and arrows.meta TikZ libraries should be called as well. Also, since we want to be able to use LaTeX's math mode, we need to call the amsmath package. In total, we have the following code snippet at the beginning of the document:
Out of personal preference, we will be using the Times New Roman 12 point font with a 1.25 line spread (which corresponds to a one-and-a-half line spacing). So we will be using this document preamble:
2. Outlining the axes
To begin, we need to draw the axes on which our economic graphs will be drawn. Since pgfplots is a dependency of TikZ, we need to open and close the TikZ environment with \begin{tikzpicture} and \end{tikzpicture}. Within this environment, to construct the pgfplots environment, we insert \begin{axis} and \end{axis}. Since, presumably, we want the economic graph to be in the center of the page, all of this should be in the center environment, with \begin{center} and \end{center} encompassing the code. So we have:
For the axis environment, parameters affect the whole graph (i.e. scaling, axis ticks, grid lines) while commands impose specific plots (i.e. functions, lines, coordinate points). One thing to note, syntactically, is that parameters are separated by commas — "," — while commands are separated by semicolons — ";".
2.1. The axis environment
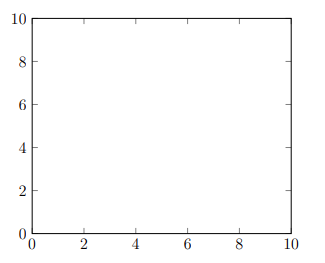
Before we can begin plotting functions, we need to specify which region of the Cartesian plane we wish to display. To specify the domain, we use the parameters xmin = 0 and xmax = 10, where 0 and 10 are the minimum and maximum bounds of the domain. Similarly, to specify the range, we use the parameters ymin = 0 and ymax = 10 to specify the minimum and maximum range bounds respectively. So far, we have this code for the basic outline of the graph:
Running this code produces Figure 2–1.
2.2. Axis line directions
We need to make a couple modifications to make this suitable for economic graphs. The default style of the graph frame is boxed, where black lines surround the graph on all sides. While this is good for line graphs and scatter plots — what pgfplots was built in mind for — economic graphs generally have an L-shaped frame. To change the frame style, we need to use the parameter axis lines = style, where the style can either be left, right, center, box, or none. Figure 2–2 shows some of these styles for the axis lines.
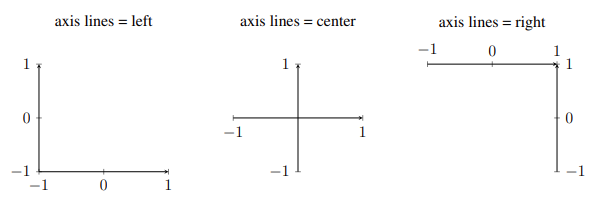
Clearly, we need to use axis lines = left as a parameter to make the L-shaped frame most economic graphs have. In addition, the arrows at the end of the axes can be removed by appending an asterisk to the end of the axis lines so we use, axis lines* = left.
2.3. Axis ticks, scale, and clipping
Economic graphs typically do not have numbers running along the axes. This is because most of them are theoretical diagrams and apply irrespective of the orders of magnitude involved. To this end, we need to remove the lines and numbers running along the x and y-axes — which are called axis ticks and axis tick labels respectively. The parameters that do this are xtick = {tick numbers} and ytick = {tick numbers} for the x and y-axes respectively. Within the curly braces after the xtick and ytick parameters, we put a list of numbers separated by a comma which we want to run along the respective axes. Since economic graphs, for the most part, keep the zero at the bottom-left, we will keep it in the x-ticks as such xtick = {0}. Since we want no axis ticks on the y-axis, we write ytick = \empty. The case of an empty axis ticks numbers list is a special case. Because pgfplots would use the default axis ticks if we had nothing within the curly braces, we need to specify that it is empty with \empty. To make non-blank axis lines — for instance, graphs with specific, empirical values — Section 4: Empirical curves covers grid lines and axis ticks.
Considering the size of the figure on the page, the default size is slightly too small to present much illustration without cluttering the space available. To slightly increase the size of the graph, we write the parameter \scale = 1.2. Of course, if you have a more complex or important illustration, a greater factor can be used to create bigger graphs. On the other side, a lesser factor can be used to create smaller graphs. A scale factor of 1.2 occupies about a third of the page.
The last parameter we need to add is clip = false. Normally, pgfplots cuts off any plots outside the graph, which is useful for automatically bounding functions. However, we want to be able to put labels outside the graph, so we disable that feature with this parameter. Instead, we will be manually indicating the domain and range of plotted functions.
2.4 Axis labels
Finally, the last consideration we have to address before plotting anything on the graph are the axis labels. It is more convenient to put them at the ends of axes instead of conventionally at the bottom (for the x-axis) and to the left (for the y-axis) because we want to use that space for other things (such as variable labels and dimension lines). To put labels at the end of the x and y-axes, the commands take the form of:
As a reminder, semicolons should be at the end of these lines because they are commands as opposed to the parameters that have been used thus far. (Subsection 3.5: Labelling explains why this command works in more detail.) For the demonstration, we will use the x and y-axis labels of $x$ and $y$ respectively. Putting the dollar signs around the x and y puts them in LaTeX's math mode, allowing us to write the mathematical expressions LaTeX is known for.
After all of these considerations are addressed, we end up with Figure 2–3:

Now the graph is ready to have plots (e.g. functions) drawn upon it. The code that produces Figure 2–3 is as follows:
3. Plotting, colours, and labelling (ex. indifference map and budget constraint)
With our axes, we can begin drawing on the graph. Suppose we wanted to illustrate why demand is downward-sloping — meaning that quantity demanded falls as price rises — using indifference curves. More specifically, we want to plot an indifference map between good A and B with budget constraints showing an increase in the price of good A corresponding to a decrease in the quantity demanded of the good.
3.1 Plotting functions
First, we want to draw an indifference curve, U₁, defined by, say,
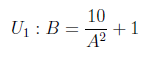
This is done by the following command:
This is a long command. Let us take this in pieces. The addplot parameter of domain = min:max restricts the function graphed to the domain bounded by the minimum x-value, min (which is 0 in this case), and maximum x-value, max (which is 10 in this case). Similarly, restrict y to domain = min:max restricts the function to the range bounded between min and max (which are 0 and 10 in this case). (Restricting y to a "domain" is a slight misnomer because the proper mathematical term for the set of y-values is "range.") Note, the reason why we need to define the domain and range, as mentioned before, is that we disabled pgfplots's clipping feature. The addplot parameter samples = n tells pgfplots to take a certain number of x-values, n, at which to evaluate the function and draw a line through all the calculated coordinates. In practice, the higher the number of samples, the smoother the plotted curve. The last addplot parameter, color = colour name, is self-explanatory. It colours the line to be the colour name. Colours are addressed in more detail in the next subsection. In Subsection 3.2: Colours, there is a list of the predefined colour names along with an explanation on how to add more predefined colour sets and define new colour names.
Moving on to the mathematical expression within the curly braces, this is where we put the function's expression, 10/(x^2)+1. It is important to note that the conventional notation of juxtaposition (placing numbers and letters side by side) for multiplication throws an error. Instead, an asterisk — "*" — can only indicate multiplication. Otherwise, conventional computer notation applies, with addition, subtraction, division, and grouping represented by "+", "-", "/", and "( )" respectively. Plotting the aforementioned command yields Figure 3–1.
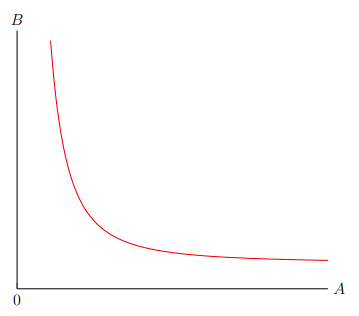
The code that produces Figure 3–1 is:
One thing to notice about Figure 3–1 and its code is that the x-axis label is A and the y-axis label is B. This is because, in this example, we want to show that an increase in the price of good A causes a decrease in the quantity demanded of the good.
Naturally, an indifference map contains more than one curve. So, let us plot multiple curves by translating the first curve to the right by one unit and up by one unit. In transformation notation, this corresponds to (x, y)→(x−1, y+1).
Successively using this transformation on U₁ produces U₂, U₃, U₄, and U₅,
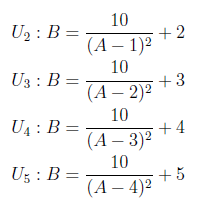
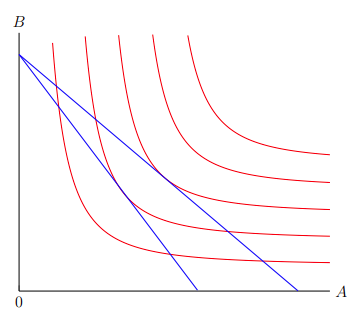
Plotting all five of these curves yields Figure 3–2.
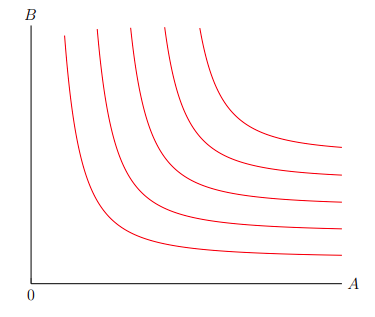
The indifference curves in Figure 3–2 are plotted by the following code snippet:
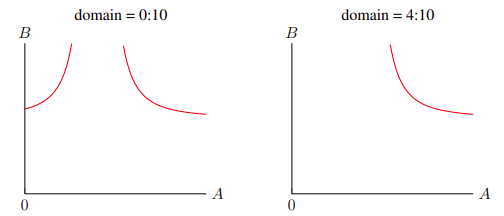
Note that the domain restrictions are different for each function. U₁ is restricted to A ∈ (0, 10), while U₂ is restricted to A ∈ (1, 10), and U₃ is restricted to A ∈ (2, 10), and so on. The reason for this is because each indifference curve's equation has different vertical asymptotes, with it being A = 0 for U₁, A = 1 for U₂, and A = 2 for U₃, etc. Because we only care about the graph of the equation at the right-hand side of the vertical asymptote, we restrict the utility functions to the domain right of the vertical asymptote. Figure 3–3 illustrates this domain restriction.
Now that we have the indifference map plotted, we need to plot the changing budget constraints in response to a rise in the price of good A. In effect, this means two diagonal lines: one from a positive B-intercept to a positive A-intercept, and another line from that B-intercept to a reduced positive A-intercept. This represents the change in the maximum number of good A that can be bought because of a price increase, while the maximum number of good B remains the same. In addition, because we want to show the change in the consumer decisions after a constriction in budget constraint, the two budget constraints must be tangent to indifference curves. We will use U₃ to be tangent to the original budget constraint at A = 4.7 and U₂ to be tangent to the new one at A = 3.3. The original and new budget constraints are calculated to be the equations B = 9.16 − 1.02A and B = 9.16 − 1.59A respectively (these are approximations of the actual tangents). Logistically, the equations of these budget constraints can be calculated or approximated beforehand, manually or with software such as WolframAlpha or Desmos. (For example, with WolframAlpha, the original budget constraint equation can found by inputting tangent at x = 4.7 for y = 10/((x-2)^2)+3, which outputs y = 9.14744–1.01611x.) Using the same addplot command which we used previously to plot the lines of the indifference curves, we can plot the two budget constraints.
Lastly, to make the budget constraint lines stand out in the midst of the indifference map, we need to thicken them. This is done by adding the parameter thick to the addplot. The preset line thicknesses are ultra thin, very thin, thin, thick, very thick, or ultra thick — or we could define our own thickness with the line width = width parameter where width is in units of length. In total, we have the following code snippet for the budget constraint lines:
Plotting them on the graph yields Figure 3–4.
3.2. Colours
In the previous subsection, we used two colours — red and blue — to draw functions. You might be wondering how many colours we can use, or how to define new colours. Remember, we called the xcolor package because it expands LaTeX's limited base capacities to manipulate and use colours.
There are 19 default colours predefined by LaTeX:

(I explain how to make these coloured squares in Subsection 6.2, the command that produces a red square is \fcolorbox{black}{red}{\textcolor{red}{\rule{\fontcharht\font`X}{\fontcharht\font`X}}}.)
However, if these colours are too limited, xcolor comes with a variety of options that defines more colours. For example, the dvipsnames option defines 68 more colours:

It is important to note that these colour names are case-sensitive. Meaning that color = violet is different from color = Violet, and color = VIOLET will throw an error.
To add the dvipsnames colour palette, we call the xcolor package with the dvipsnames option, so, \usepackage[dvipsnames]{xcolor}. If the usepackage command is called after pgfplots's, an error will be thrown. This is because TikZ calls xcolor by default and clashes with this new usepackage command. So make sure that the xcolor package is called before the TikZ package. Alternatively, if this does not work, then we could add the parameter xcolor = {dvipsnames} to the document class command. For us, we would use, \documentclass[12pt, xcolor = {dvipsnames}]{article}.
There are other palettes aside from dvipsnames, such as svgnames, which defines 151 colours, or x11names which defines 317 colours. In addition, new colours can be manually defined using the command \definecolor{name}{model}{variable 1, variable 2, variable 3}, where the model is either rgb, HTML, cmyk, among others. For example, a light tan colour can be defined by \definecolor {name}{rgb}{0.95, 0.95, 0.92}.
A lot can be done with colours in LaTeX. We can colour text, have background colours, and make the page colour different from the standard white (though that would be ill advised, considering the strain on printers). Most of these are outside the scope of this guide and so will not be covered. Resources are available at Section 8: Resources, which includes documentation and guides on the xcolor package.
3.3. Plotting dashed line segments
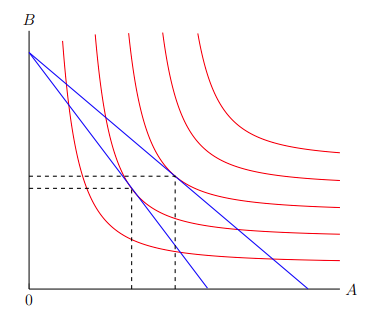
Returning to the indifference map and budget constraints graph we were working on, the next step is to draw dashed lines on it. Pgfplots has a command for line graphs, wherein it will connect all inputted coordinates sequentially with a line going through them. The coordinates of the original decision point — where the original budget constraint is tangent to an indifference curve — are calculated to be (4.7, 4.37). So the dashed line will go from (4.7, 0), the A-intercept, to (4.7, 4.37), the decision point, to (0, 4.37), the B-intercept. The command that does this is as follows:
As seen, the coordinates the line goes through should be listed within the curly braces. Also, because we want the line to be dashed, we include the parameter dashed. The other two parameters, color = black and thick have already been covered in the previous subsections. They respectively colour the resulting line black and make its line width thicker. Repeating this process for the new decision point at (3.3, 3.9) yields Figure 3–5.
3.4. Plotting coordinate points
Conveniently, imposing black coordinate points on the graph is very similar to drawing a line. In fact, to make a scatter plot, pgfplots uses the same command that was previously used to draw connected line segments. Then two parameters are added. The first is mark = *, which draws a filled circle at every coordinate the line connects. Marks other than "*" can be used, such as "x" , "+", "|", "o", (all of which look like the character representing it), and many more marks. Second, to remove the line, we write the parameter only marks. In addition, to increase the size of the marks, we add the parameter mark size = 3. In total, we have the following command to plot the coordinate points:
Using this command on the graph yields Figure 3–6.

3.5. Labelling
Finally, to finish the graph we need to label all the relevant parts of it. Specifically, we need to put letters near the A and B-intercepts, the coordinate points, and the ends of the functions. To label a part of the graph, the command takes the form of:
This command will place some text, the label, next to the coordinate specified. In addition, where the label ends up near the coordinate depends on the position, it can either be left, right, above, or below the coordinate. For instance, to put a label of Qₐ below (4.7, 0), where the dashed line extending downward from the original decision point meets the A-axis, we write the following command:
We have already used a form of the node command previously when labelling our axes. Notice, however, that the coordinate point for an axis label is different because it refers to the end of an axis. Using the labelling command to label the rest of the graph, such as the functions and coordinates, we end up with Figure 3–7.
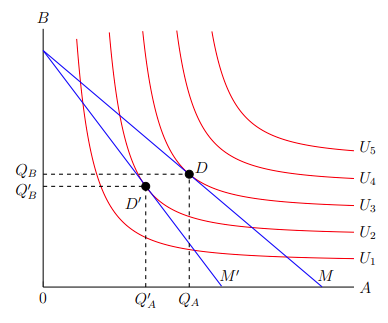
Finally, we have completed the indifference map illustrating why demand slopes downward. It is because Q′ₐ is less than Qₐ when the budget shifts from M to M′. More importantly, we illustrated this in LaTeX! Figure 3–7 is produced by the following code, combining all of the elements covered in this section:
4. Empirical curves (ex. market equilibrium)
At the start of this guide, I assumed that we were working on a blank graph. Meaning, the x and y-axis did not have any ticks because they do not have any values associated with them. These types of graphs are useful for theoretical models — applicable to relevant situations no matter the order of magnitude. Sometimes, however, we actually have empirical data. In this case, we might want grid lines on which to impose plots such as functions, coordinates, dashed lines, and so on. A couple modifications are needed to convert our "blank" graph to service empirical values. Specifically, we want to impose grid lines and then work out the legibility problems such as distancing axis labels and putting a white background colour behind labels in the graph to avoid clutter. Let us transform a market equilibrium curve, Figure 4–1, so that is able to reflect empirical data.
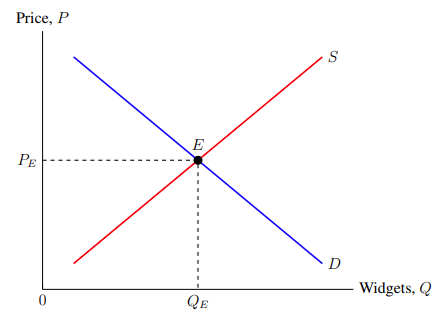
The elements in Figure 4–1 have been explained in previous sections. It is produced by the following code:
4.1. Major and minor grid lines
To start with, we want axis ticks and numbers to run along both axes. This was covered briefly in Subsection 2.3: Axis ticks, scale, and clipping, but there we were focused on removing them. As a reminder, the axis parameters which control the ticks are xtick = {tick numbers} and ytick = {tick numbers}. Instead of them containing only 0 or being empty, we want them to be the numbers which fit our data. In this case, the set of tick numbers will be {0,1,2,3,4,5,6, 7,8,9,10} for both of them. Next, we want to impose grid lines upon the graph. We are still working with axis parameters, not commands. Usefully, there are two types of grid lines, major grid lines and minor grid lines. Major grid lines extend from the axis ticks and numbers. Meanwhile minor grid lines extend from smaller ticks between major ticks and do not have a number associated with them. They both have different styles and so can aesthetically convey more precision. To show both grids, include the axis parameter grid = both. Similarly, if we want only one or none of the grids, we would use the value of major, minor, or none–though by default neither grid is shown. To set the number of minor ticks between major ticks, the axis parameter minor tick num = number is used, where the number is the number of minor ticks. In this case, we want one minor tick halfway between the major ticks — otherwise it would be too cluttered — so the number of minor ticks is 1. Moreover, we want the major grid lines to be solid lines and the minor grid lines to be dotted lines. This way, half and full increments are visually evident. To change the style of major and minor grid lines to solid and dotted lines, we use grid style = solid and minor grid style = dotted respectively. More styles include dashed, thin, and thick. Defining the grid style to be solid is redundant since that is the default, but I have opted to make it explicit. So far we have added, or modified, the parameters in the following code snippet:
This snippet adds axis ticks from 1 to 10 in increments of 1 on both the x and y axes. In addition, it shows both the minor and major grid lines, sets the number of minor ticks between major ticks to one tick, and makes major grid lines solid lines and minor grid lines dotted lines. Using these parameters to the blank market equilibrium graph results in Figure 4–2.
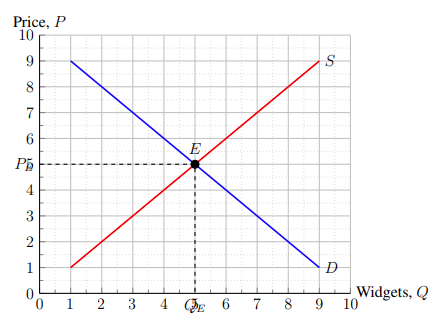
Ah! That is ugly! While we got the axis ticks and grid lines we were seeking, this caused other issues for the legibility of this graph. Specifically, the labels of Qₑ and Pₑ need to be moved away from the axis numbers, the axis labels should be moved slightly away from the graph, and the labels of E, S, and D need to have white backgrounds to reduce clutter. In addition, there are two zeros at the origin — one is enough.
4.2. Distancing labels, colouring label backgrounds
Starting with the former issue, the x and y-intercept labels need to be moved away from the graph to make room for the axis numbers. Recall that labels take the form of:
While the position does a good job in most situations of determining how far the label should be from the coordinate, sometimes we want to increase this distance. In such situations, the distance can be specified with position = distance. So, for example, the position for Qₑ can be changed to below = 10pt. Repeating this for the Pₑ label, we have the following code snippet:
Moving on to the latter issues. Getting rid of the y-axis label of 0 and moving the axis labels can both be done by changing the domain and range of the graph shown. To get rid of the 0 on the y-axis, we define the minimum of the range to be 0.01 (any very small number suffices, though this varies depending on the order of magnitude of the data). So we have ymin = 0.01 as an axis parameter. To distance the axis labels, the maximums of both the domain and range should be extended to 10.5 (this too varies depending on the order of magnitude). In sum, we have the following code snippet:
Finally, we want to colour the background of labels on the graph white. Otherwise, we would be stuck with lines cutting through E, S, and D, which does not look good. This also involves a relatively simple adjustment. We add the parameter fill = white to the node commands of the labels. The code snippet for the changed labels are:
The label of E has also been distanced by 5 pt using the positioning parameter as explained in the preceding paragraph. This was done to avoid covering the supply and demand lines with the white background. There are other ways to resolve this inconvenience. For example, because pgfplots layers these plots sequentially — where later commands cover previous ones — simply having the node command for the label above the ones for the supply and demand line curves could work. That way, the commands for the supply and demand curves would be executed after the label and would cover up the white background.
Combining all of these adjustments, we end up with Figure 4–3.
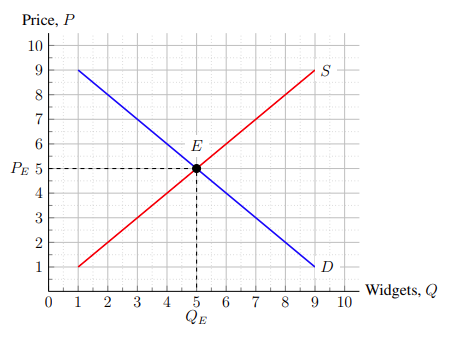
And so we have finished adjusting the blank graph to one with ticks and grid lines so that it can accommodate empirical data and represent specific values. The code for Figure 4–3 is:
5. Shading, arrows, and graphs side by side (ex. supply increase, price-taking firm)
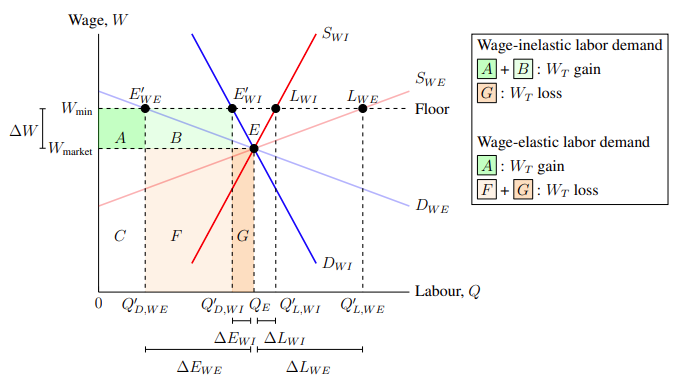
A lot can be done by plotting curves, lines, and coordinate points. But sometimes we need to point out features or indicate areas on the graph. This can be done by drawing arrows and shading in areas on the graph with colour. Let us use these tools to illustrate the bumper harvest paradox: why farmers' incomes fall after a bountiful harvest. A bumper harvest corresponds to a supply shift rightward in the market equilibrium graph where demand is relatively price-inelastic. This is depicted in Figure 5–1.
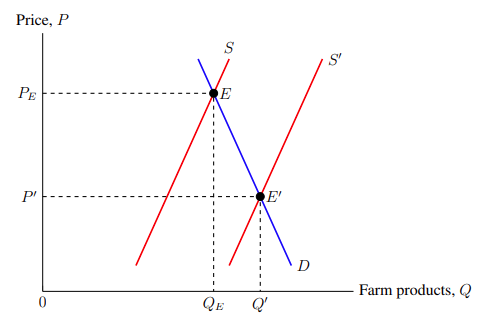
Figure 5–1 is graphed using the tools already explained in the sections above. The code is as follows:
5.1. Opacity and transparency
Right now, both supply curves are the same opaque red. To make it evident which is the original supply curve and which is the new one, we will make the new one slightly transparent. We do this by adding the parameter opacity = opacity value to the addplot command, where the opacity value is the percent the plot is opaque ranging from 0, perfectly transparent, to 1, perfectly opaque. Making the new curve mostly transparent seems to make it evident that it is new. So we write opacity = 0.3 for its addplot command. The result of making the new supply curve more transparent is shown in Figure 5–2.
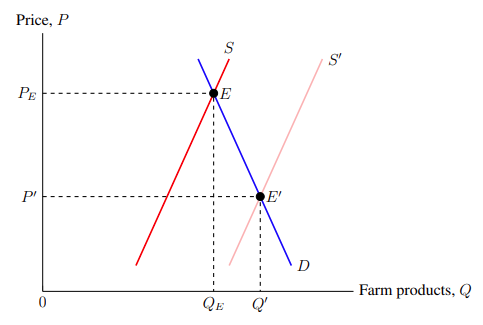
It is important to note that the xcolor package — which was mentioned in Subsection 3.2: Colours — offers a more concise though slightly less readable way of making colours transparent. When using a colour, an exclamation mark can be used after the colour name, right after which comes the opacity value — colour name!opacity value. This one ranges from 0 being perfectly transparent to 100 being perfectly opaque. For example, red!10 is mostly transparent, red!50 is half transparent, and red!90 is mostly opaque. (Although, if I might add, that "mostly transparent red" looks more like salmon.)

5.2. Shading in boxes with colours
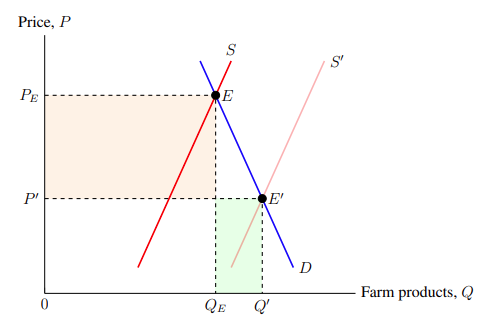
Now that we have distinguished which supply curve is the new one (more than just using the label S′), we also want to indicate the areas that represent the total revenue loss and the total revenue gain for the farmers. That way, we can graphically show that the loss in total revenue is much greater than the total revenue gain. The command that fills in an area on the graph with colour takes the form of:
In this command, (A), (B), (C), . . . , are an indefinite number of coordinates. The command colours in the polygon defined by the coordinates with the specified colour. Looking at the graph, the original equilibrium point is (5.5, 7.67) and the new equilibrium point is (7, 3.67). Meaning that, for the loss area, we need to colour in orange the square defined by the coordinates (0, 7.67), (0, 3.67), (5.5, 3.67), and (5.5, 7.67). Similarly, we shade green the gain area defined by the coordinates (5.5, 0), (5.5, 3.67), (7, 3.67), and (7, 0). So far, we have the following code snippet:
Since we want these coloured areas to be unobtrusive, the colours need to be mostly transparent. This can be done the same way it is done to plots as shown in the previous subsection, Subsection 5.1: Opacity and transparency, either through TikZ's opacity parameter or through xcolor's exclamation mark notation. So the snippet the graph will be using is:
Unfortunately, we cannot simply put these commands into the axis environment. There are a couple considerations to address so that these coloured areas do not interfere and overlap with other features on the graph. Because pgfplots processes commands sequentially so that later plots are layered upon earlier plots, the fill commands should precede every other one — otherwise the coloured areas could cover up another part of the graph. Also, since fill commands cannot precede the axis parameters, the axis parameter axis on top should be added. This ensures that the axis lines are not covered up by plots and other commands. The coloured areas are shown in Figure 5–3.
5.3. Straight and curly arrows
While this graph illustrates the bumper harvest through the relative sizes of the shaded areas, it is missing information about what those shaded areas represent. Of course, a reader could infer from context that the orange area represents the total revenue loss and the green area represents the total revenue gain, but we can also make the graph more readable for them. So let us label the shaded areas with curly arrows. Also, since we want to illustrate the supply curve moving from the original to the new one, we can draw a straight arrow from the original to the new curves.
Starting with the latter, since that is easier, the command for drawing arrows takes the form of:
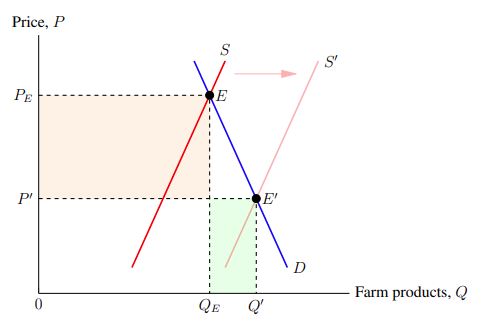
This command draws an arrow starting from (A) and ending at (B). The tip of the arrow at B is specified by the arrowhead value. TikZ has a limited array of arrowheads to choose from, so that is why we loaded the arrows.meta TikZ library in Subsection 1.3: Packages. With this library, we have access to more arrowheads such as Triangle, Circle, Square, Diamond, and so on, all of which are self-descriptive. The Triangle arrowhead is the most appropriate to show the shift from the original to the new supply curves.
Using this command, we will draw an arrow from the right of the original supply curve to the left of the new supply curve. This corresponds to an arrow from (6.3, 8.5) to (8.3, 8.5) with an arrowhead of Triangle. So we have the following code snippet:
While this will do the job, there are a couple changes we should make to improve the aesthetics and readability of the arrow. First, it would be better if the arrow was a mostly transparent red to show it is modifying the supply curve. Conveniently, this is just like filling areas with colours and colouring plots as we have done in before. We write red, opacity = 0.3 as parameters to the draw command for the arrow. Second, arrowheads are small by default. We would like to make the supply curve shift arrow slightly bigger. This is slightly harder to do. To begin with, we surround the arrowhead value with curly braces to indicate that we are using a custom arrowhead. So we have -{Triangle}. Then, as parameters to the arrowhead value we add the parameters length = 4mm, width = 2mm which modify the dimensions of the arrowhead. Accordingly, we have the final code snippet for the supply shift arrow:
Using this command to draw the arrow upon the graph results in Figure 5–4.
Next, we will label the gain and loss areas. Simply putting a vertical arrow from below the x-axis to the green area would be too cluttered. We would have the labels Q, Q′ , and an arrow all sharing that small space. Instead, let us draw a curly arrow pointing from the bottom-right of the axis to the centre of the green area curving in a counterclockwise direction so that it avoids the Q and Q′ labels. Curly arrows are drawn with a draw command in the form of:
Notice that this is nearly identical to the command for straight arrows, except for one addition. Within the square brackets after the "to", the parameters specify the angles from the starting coordinate and to the ending coordinate which the line for the curve should be drawn. They are given in arc degrees, meaning from 0 for right, to 90 for up, to 180 for left, to 270 for down, to 360 for right again, and everything in between. I have found beforehand that the starting coordinate for the curly arrow is (10, -1.5) and the ending coordinate is (6.5, 0.7). Since the arrow should spring forth upward from the starting coordinate and comes into the ending coordinate from the right, the out angle is 90 and the in angle is 0. And so the code snippet producing the curly arrow pointing at the gain area is:
Repeating this for the loss area, for an arrow from the top to the orange box, and adding text labels (which was covered in Subsection 3.5: Labelling), we have this code snippet:
Combining the straight and curly arrows, Figure 5–5 is produced.
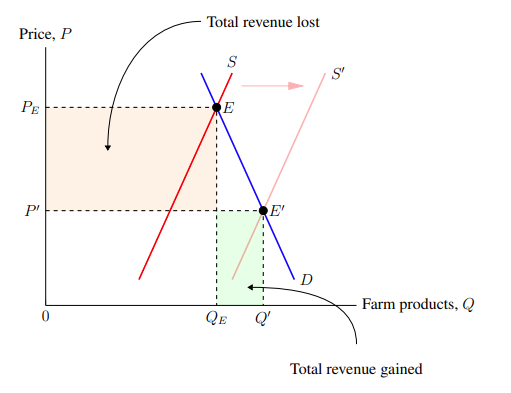
Figure 5–5 is produced by the following code:
5.4. Arranging graphs side by side
In economics, it is common to arrange the market equilibrium graph to be side by side with the price-taking firm graph. This is useful to show how shifts in the market sets the price with which individual firms need to operate. More generally, we will use this example to demonstrate how we can place graphs beside each other. Suppose we wanted to show how the downward price movement in the market equilibrium causes a decrease in the total economic profit for individual farmers. The price-taking graph of this scenario is shown in Figure 5–6.
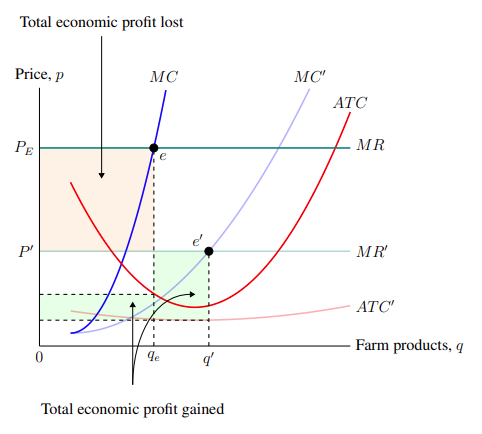
The above graph is produced entirely with the tools and techniques already covered in previous sections. It is a combination of plots, coordinate points, labels, colours and transparency, and so on. Figure 5–6 is produced by the following code:
We want it arranged such that the market equilibrium graph (Figure 5–5) is on the left-hand side of a panel while the price-taking firm (Figure 5–6) is on the righthand side. Surprisingly, this is actually very simple. All we need to do is create another axis environment right after the first one, but still within the same tikzpicture environment. This will overlay the two graphs on top of each other. Then, we add the parameter shift = (axis cs: x-shift, y-shift) to the second axis environment where the x and y-shifts are the amounts by which the second graph will be moved away from its original position. Since we want to shift the second graph (the price-taking firm) to the right of the first graph (the market equilibrium), we will use an x-shift of 17 and a y-shift of 0. So we have:
Finally, we need to make an adjustment to fit the figure on the page. Since the figure's width is greater than what the page margins allow, we tell TikZ to disregard the page margins by widening the picture frame. To do this, we write \hspace*{-3cm} before the \begin{tikzpicture} and after the \end{tikzpicture} which widens the picture's frame to the left by 3 cm and to the right by 3 cm respectively. In total, putting all of this together yields Figure 5–7.
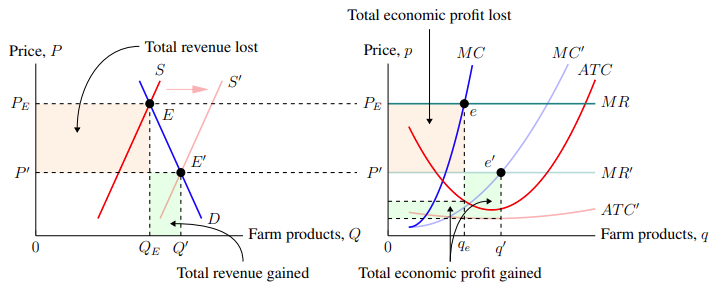
The code that produces Figure 5–7 is:
The code is executed using the commands and parameters that produce Figures 5–5 and 5–6 for Graphs 1 and 2 respectively. (Again, the full code for Figure 5–7 can be accessed on the GitHub repository https://github.com/jackypacky/pgf-econ-graphs.)
5.5. Shading in the area under a curve
Closing off this section, we will briefly discuss how to shade the area under a curve — and by extension, how to shade in area between two curves — since that was not covered in the previous example. Suppose we wanted to shade in the area under a production-possibility frontier between good A and good B with a transparent blue in order to illustrate the output possibilities that exist which are not necessarily efficient. The production-possibility frontier is illustrated in Figure 5–8.
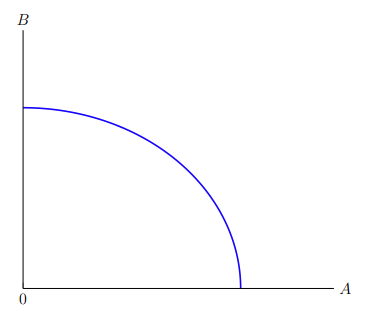
The code that produces Figure 5–8 is:
To shade in areas between two functions, we use a command that takes the form of:
where parameters are the parameters which modify the addplot command, and f and g are the name paths of the functions. For the parameters, we will use blue, and opacity = 0.1 which creates a transparent blue similar to what we did in Subsection 5.1: Opacity and transparency.
To input the name paths f and g, however, we first need to define the name paths beforehand. To define the name path of a curve, we add the parameter name path = label to the addplot command where label is the name we want to assign it. So we will use the addplot parameter name path = frontier for the command which plots the production-possibility curve. Since we need another function between which we can shade in the area, and since we want to shade the area under the curve, we need to plot a new curve defined by the equation y = 0 and name it axis. For this new axis curve, we add the addplot parameter line width = 0pt to make it invisible — since we do not want it to show up on the graph.
In total, shading in the area under the production-possibility curve is shown in Figure 5–9.
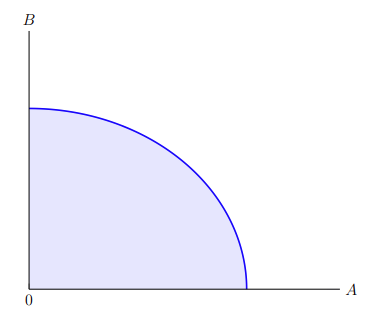
Figure 5–9 is produced by the following code:
6. Axis dimension lines, line breaks in labels, and a legend (ex. excise tax)
Continuing our discussion on enhancing the readability of graphs, let us now impose dimension lines and a legend upon a graph. Instead of putting a label on a graph pointing to the coloured areas, we could have instead added a legend showing what each area represents. In addition, to indicate what the differences between two axis labels are and mean, dimension lines can be used. Dimension lines are lines used in graphs, figures, and drawings to indicate sizes, quantities, and distances — dimensions. At each of the ends of dimension lines, there is a perpendicular line joined to it like a "T". (Dimension lines kind of look like this: "| — –|".)
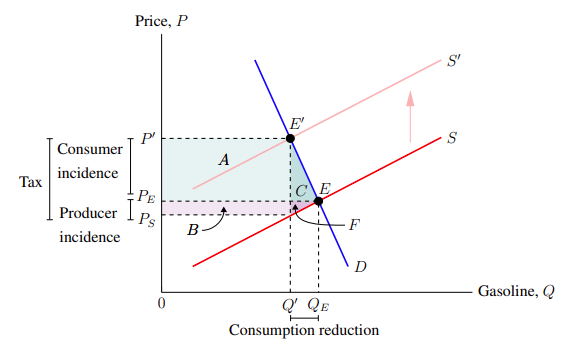
We will use an excise tax graph to illustrate the usefulness of dimension lines. Suppose we wanted to illustrate the tax incidence of an excise tax on gasoline. This is shown in Figure 6–1.
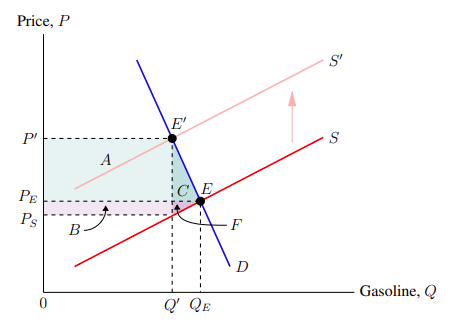
The code that produces Figure 6–1 is:
6.1. Adding dimension lines and line breaks in labels
Dimension lines are added in an identical manner to which arrows are drawn. Recall that the command for an arrow takes the form of:
What I did not tell you was that arrowheads can be appended to both the end of an arrow and the start of an arrow. So the arrow with an arrowhead at its tail and head takes the form of:
Dimension lines use the arrowhead "|", which is a nice symbolic description of how the arrow looks. We have:
The difference between Qₑ and Q′ is the reduction of the quantity of gas consumed after the imposition of the excise tax. To illustrate that on the graph, we will draw a dimension indicator from the bottom of Q′ to Qₑ. Below this, we will add a label with the text "Consumption reduction." Since Q′ is at Q = 4.14 and Qₑ is at Q = 5.05, we have:
We would like to repeat this for the consumer incidence — between Pₑ and P′ — and the producer incidence — between Pₛ and Pₑ. However, simply copying the above would not work because the label width would be too large. Instead, we need a way to insert a line break between the two words in both labels. This is done by adding the parameter align = left to tell how the stacked text should align (either left, right, or center), and by adding two backslashes — "\\" — where we want the line to break. Accordingly, the code for dimension lines and labels for the consumer and producer incidences is:
Adding a dimension line from Pₛ to P′ representing the total tax and adding all of the dimension lines and labels mentioned so far results in Figure 6–2.
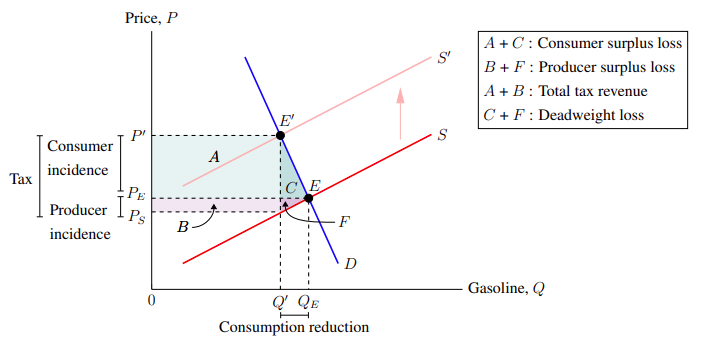
6.2. Adding a legend
Using a legend, we can specify what the areas A, B, C, and F represent on the graph. Adding a legend combines a couple of the commands and parameters used in the last subsection. While pgfplots has its own inbuilt legend feature, it is rather unwieldy to use. Instead, we are going to use a text label and put it at the top-right of the graph. The label should allow line breaks and have a black border drawn around it. So we will use:
Recall that adding the parameter align to the node command allows line break — using \\ — to be used within the label. Also, since the align is set to left, text lines will be flushed to the left. These were covered in the previous subsection. What is new, however, is the draw node parameter, which draws a black border around the label. In the command, the top-left of the legend will be at (10.5, 10), which corresponds to the top-right of the graph — where we want the legend to go. Adding text that describes what the areas represent, we have:
Using the above node command to add a legend to the graph, we get Figure 6–3.
As it stands, the legend looks a bit boring. To improve the aesthetics of the legend, we could add a colored background to the letters A, B, C, and F, to visually connect it to the coloured areas which they point to. It would look good if A were coloured a very transparent teal, B were coloured a very transparent violet, and so on.
Fortunately, the xcolor package has a command to do exactly that. The xcolor command to add a coloured background to text takes the form of:
In this command, the frame colour is the colour which surrounds the edges of the coloured background. The background colour is the colour behind the text. For the A text in the legend, since we want its background to be a very transparent teal, the command we want is:
Notice that the command does not end with a semicolon, this is because it is not a TikZ command.
While the A looks fine, the widths of the background colour is determined by the widths of the text within it. So we hit a snag when using multiple background colours for texts with varying widths. For example, the background colour for M is wider than the one for l. Beside each other, the inconsistent widths are noticeable. To fix this, we will use the makebox LaTeX command (\makebox[width]{text}) with the width of the height of "X", (\fontcharht\font`X). Meaning the command we will be using to make a coloured background for the letters is:
which is quite overwhelming to look at without processing it in parts.
You may be unfamiliar with the grave accent, " ` ". On a conventional US keyboard, it is located at the top-left. It is used in LaTeX for an assortment of purposes, including quotation marks and adding a grave accent to characters. (For example, adding a grave accent to "a" using \`a produces "à".)This way, M is just as wide as l. Unfortunately, controlling heights is much harder and I will skip it in this guide. If we wanted to just have a coloured box with no text in it, we would use:
Running the above command produces a transparent teal coloured box.

This works because \rule{width}{height} generates a rectangular blob of ink. Incidentally, this is how I have been presenting the colours on their own throughout this guide. Finally, because adding a legend often makes a graph's width bigger than what the page margins allow, we add \hspace*{-3cm} before \begin{tikzpicture} and after \end{tikzpicture}. We also did this in Subsection 5.4: Arranging graphs side by side when we encountered the same problem.
In total, we have the following code snippet for the legend:
Adding this to the graph, we get Figure 6–4.
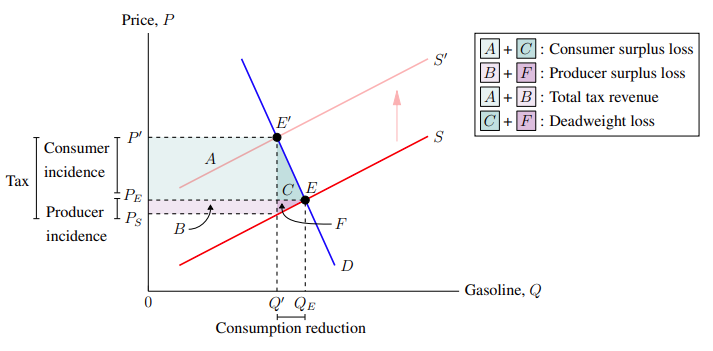
And viola! We have added dimension lines and a legend, further communicating what different sections of the graph mean. Now, anyone looking at this graph would pictorially understand that consumers bear the bulk of the tax incidence and the surplus loss from a gasoline excise tax — and why. (Assuming that supply is relatively price-elastic and demand is relatively price-inelastic.) The code that produces Figure 6–4 is:
7. Conclusion
With this toolbox, you can create virtually any economic graph. The effort to learn pgfplots and LaTeX is worth it. While on one hand, most word processors such as Google Docs (with Google Sheets) and Word (with Excel) can provide the necessities of economic graphs — axes, lines, curves, and labels — pgfplots has more flexibility, from shading areas, to adding dashed lines, and to adding dimension lines. All done in style.
Of course, since it is LaTeX, this is only the tip of the iceburg. Everyone stands on the shoulders of giants. First, Donald Knuth created TeX to typeset documents. Then Leslie Lamport created LaTeX as a markup to TeX. Then Till Tantau created TikZ on top of this foundation to create graphics. After, before, and between this sequence is a list of many other contributors to the giant on which we stand. Finally, we come along and, with serendipity, find out that we can create beautiful and sleek graphs for economics.
Yet, we can always do more. For instance, we could automate the graph creation by defining variables and automatically calculating the points of intersection. That, however, is outside the scope of this guide.
If I have done my job successfully, you have partially scaled LaTeX's reputable learning curve in this one domain of making graphs. If I have not, you have been left abandoned, with no guidance on how to begin your ascent (at least, not from me!). Let us hope for the former.
8. Resources
Getting started with LaTeX and learning
- TeX Live: http://www.tug.org/texlive/. This is a portal to install TeX, the TeXworks IDE, and a few ubiquitous packages (including pgfplots and xcolor).
- Overleaf: https://www.overleaf.com/. If installing LaTeX is too much of a commitment, there are many online LaTeX editors that are sufficient for this guide. Overleaf has pgfplots and xcolor already installed, so you do not need to worry about that. On the subject of pricing, they offer a free version which contains all the essentials and only lacks a few specialized features such as GitHub integration or real-time collaboration.
- LaTeX on Wikibooks: https://en.wikibooks.org/wiki/LaTeX. This guide explains the basics of how LaTeX works. From installing LaTeX, to making a document, to more technical aspects such as boxes, the Wikibook has its explanations and accompanying code.
- TeX-LaTeX Stack Exchange: https://tex.stackexchange.com/. Stack Exchange is a forum where people can ask and answer questions. This subforum specifically deals with LaTeX, which includes pgfplots. Of course, if you have a question, first use the search feature to check if it has been answered before. Then, read the rules and ask away.
Pgfplots and TikZ guides
- Pgfplots package guide by Overleaf: https://www.overleaf.com/learn/latex/Pgfplots_package. Pgfplots was designed to make line graphs and scatter plots. We had to adapt it for economic graphs. But if you want to use pgfplots for more conventional purposes, read this guide by Overleaf.
- Usepackage{TikZ} for economists by Kevin Goulding: http://static.latexstudio.net/wp-content/uploads/2016/06/tikzforeconomists-110619150244-phpapp01.pdf. This is another guide on making economic graphs in LaTeX. It uses TikZ, however, and was written before pgfplots was released. Since pgfplots is a dependency of TikZ, the code explained in Kevin Goulding's guide may be applicable to making economic graphs with pgfplots.
Package installation links and documentation
Although the LaTeX editing solutions above — TeX Live and Overleaf — already have these packages pre-installed, if you do not have these packages or want the latest versions, you can access them at these CTAN links. Also, package manuals are available on CTAN, but beware they are hundreds of pages of technical documentation.
- Pgfplots package on CTAN: https://ctan.org/pkg/pgfplots. This pgfplots package installation link also comes with TikZ.
- Xcolor package on CTAN: https://ctan.org/pkg/xcolor.
9. Other examples
Again, all of the finished graphs in this guide — the PDFs and the code — are available on the GitHub repository, including the examples below. The repository can be accessed at https://github.com/jackypacky/pgf-econ-graphs.
How to Draw a Line Graph in Latex
Source: https://towardsdatascience.com/using-pgfplots-to-make-economic-graphs-in-latex-bcdc8e27c0eb
0 Response to "How to Draw a Line Graph in Latex"
Post a Comment